Introduction

The concept of reputation function plays a pivotal role in assessing immutable merit. Persistent Identities generate Web3 Footprint - the totality of data points generated by a real-world person on-chain. Simply put, Reputation functions are slices of one's Web3 footprint evaluated for a particular purpose be that one's credit rating, academic achievement, applicability to be a member of a given DAO, one's reputation as a founder, etc. Although there are some limits to the number of use cases of reputation, there is an infinite number of possible reputation functions.
Reputation scores are variables that a reputation function consists of. Age of account, number of X posts, time-weighted liquidity provided to a dApp - all these are examples of reputation scores. Technically, a reputation function aims to aggregate specific reputation scores, condensing factors such as importance, value, and difficulty, into a single metric.

So what are the desired mathematical properties of Reputation Functions, such that these functions can both reward and incentivize as broad a spectrum of economic activities as possible? In what follows we will perform a more formal derivation of a generalized reputation function. Before that, however, we would like to summarize our considerations when designing it.

Henceforth, we will be using the concept of Galactica.com meritocratic UBI distribution when giving examples of a process to be optimized using Reputation Functions. The core idea is simple - a tokenized diversified portfolio of assets is distributed across all Citizens of Galactica.com to both incentivize and reward positive contributions to the network.

An important consideration for anyone designing incentive mechanisms should be the system's propensity to a concentration of resources one tries to distribute, be it money, power, status, or some other sort of social capital. In the end, we, the people of the web3 space are no strangers to ill-designed incentive and distribution systems. Therefore, to ensure fairness and prevent monopolization by early adopters, certain considerations must be addressed. These considerations include but are not limited to:

• Bound reputation: firstly, it's crucial that specific reputations, as well as the total reputation, have upper bounds. This prevents disproportionately large reputation scores from skewing the system, especially in the early distribution stages. In other words, there must be some sort of decreasing returns to work performed. In this case, there will eventually be an asymptote towards which the Reputation converges.

• Dynamic reputation: additionally, distinguishing between active participation and inactivity is essential. While an additive point system is intuitive, inactive users' scores should slowly dilute away in favor of active participants.

• Time decay within specific reputation functions: this penalizes inactivity among early adopters while allowing any users parity through sustained effort and skill.

• Democratic reputation: creating a total reputation function presents its own set of challenges, primarily due to the diverse needs of the community. While the technological stack of modern blockchains enables the creation of reputation functions based on statistical and elementary functions, determining the most appropriate total reputation function requires community input and democratic decision-making.

• Predictability of incentives: furthermore, the total reputation function must be predictable, ensuring that users understand which behaviors are most rewarded.

• Static vs Dynamic Pay-offs: it's important to differentiate between one-off and continuous pay-off functions, with one-off rewards being fixed and continuous rewards decaying over time.
  

Ultimately, the total reputation comprises both one-off and continuous pay-offs, with the latter subject to time decay. For example, considering the Galactica.com UBI distribution, by incentivizing users (with UBI) to align with the network goals (reputation scores), the total reputation function serves as a mechanism for preserving meritocracy.

However, it's crucial to recognize that incentives may evolve, requiring flexibility in defining the total reputation function as an increase per block rather than in absolute terms. This approach ensures that users who best align with the current incentives can earn a reputation at an optimal rate based on their ongoing contributions to the network.

Context and Definitions

First off, let us introduce some definitions:

• Reputation type: Total reputation is a function of work done. Different types of work are collected in different types of reputations. This definition is only of practical importance but does not have an input to the model itself.

• Action/Task: The only way that one can quantify work that has been done is through verifiable proofs of work within predetermined conditions that are tied to predetermined rewards.

• Table: A list of all actions/tasks within a reputation type,

• Weight: A number that specifies the sensitivity of a global reputation function to incremental units of work done. Each reputation type has a weight within total reputation.
  

How can one translate work done to a simple number? There is no way to consistently incentivize people other than a framework mapping actions into rewards. Coincidentally, mathematically it is the same as a rating or a reputation system - the only difference being that reputation works ex-post, while incentive system - ex-ante. Actions that users can perform must be listed in advance and they must have specified rewards after completion.

Let us consider an average user within any type of incentivized system - e.g. an airdrop campaign. Our user can distribute one's time to perform work and achieve certain tasks within a given timeframe. Said work can be distributed towards finishing different tasks thus advancing different reputation types - e.g. liking a tweet made by the project running the campaign - part of X's (formerly Twitter) reputation.

Energy/time/work the user spends can be proxied by the number of tasks accomplished within a given time-frame. Furthermore, when using such a proxy, the user's competitiveness in said work is also taken into account since higher skill yields more results. In the end, people who invest their time working, are going to gain more points, and people who are proficient in their work are going to be rewarded even more, since they can finish a higher volume of quality work within the same period.

Thus, it is fair to say that reputation points are a proxy value for the amount of qualitative work performed.

If the tables (a list of all actions/tasks within a reputation type) are created in an ideal fashion (so that points ideally correspond to the value of qualitative work - units of work normalized for time and value) and the user doing the work is ideal the functions of time distribution in real life and point distribution in the space of reputation types are the same. Since time distribution is a plane on which all times add to a constant (approximately, since the problem is discrete rather than continuous), mathematically speaking this surface is a plane that is angled at 45 degrees to each of the axes - the iso-work plane, see Figure 1.0.

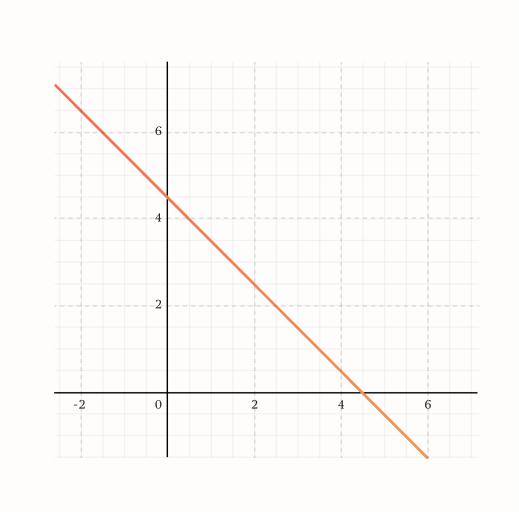
Figure 1: Iso-work plane for 2-dimensional space

It is necessary to add a note that real users are far from ideal ones. Their distribution, in reality, will be different from the ideal case since no one is proficient in all different kinds of tasks, thus their distribution of points is always going to be below the ideal case.

Reputation functions can be thought of as incentive systems - systems that incentivize a particular behavior. The generally desired property is that the highest rewards are earned by those who are aligned with the protocol's incentives.

Rewards are represented with weights and they should incentivize people to invest their time in the desired ratios across the activities underlying reputation types. Those who comply with this rule will be rewarded the most. Imputed work is additive thus the function should reward the most those people who have their work distributed in proportion to the desired weights.

A Formal Model of Reputation

Let us introduce some mathematical grounds that will be used later. If there are N distinct types of reputation (tables that convert user's work to points) every single user is represented by an N-dimensional array. Space of all possible reputation configurations is an $N$N-dimensional space ($X^N$XN) and a single user is represented as a point in this space. Reputation is a function in this space that takes points from N-dimensional space and outputs a positive real number, i.e.:

$R(x_{1},x_{2},x_{3},...,x_{N}) : X^N \to \Re^+$R(x1​,x2​,x3​,...,xN​):XN→ ℜ+

Generalized reputation functions can output a negative number if the function is bound from below. In this event, a simple linear transformation can always transform it into a positive case. If it does not have a lower bound then some users might not be incentivised to be further invested in the system. Therefore, it is best to make the reputation bounded by some lower limit and in this document, the reputation will have a lower bound of 1 for all reputation types. No meaning other than its mathematical practicality is given to this number.

It has been mentioned that a reputation system is both a reward and an incentive system. Now let us look at what that means. Looking at the community as a whole (all subjects to a given reputation function), the collection of points that represents all users that had imputed the same amount of work W is represented by the function:

$W = x_{1} + x_{2} + ... + x_{N}$W=x1​+ x2​+...+ xN​

This can be illustrated in the case of 3 variables:

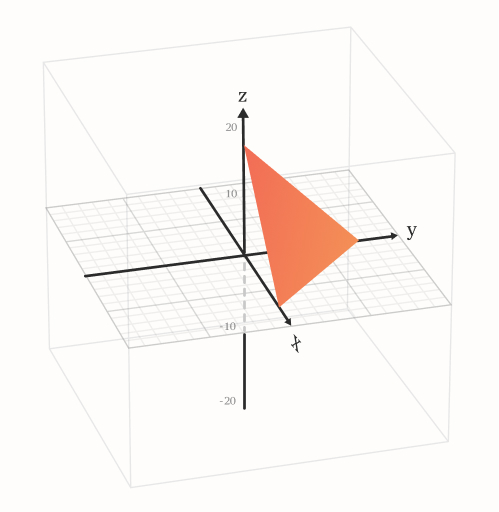
Figure 2: Iso-work plane in N=3 dimensions

If the function is predictable, for every W, there is a point that has the largest reward. Because the work is additive, the simplest incentive function is the line because it requires people to keep fixed ratios of work as they accumulate reputation points. Incentive lines defined in this way, have fixed incentives independent of how much work has been done by the users.

Let us introduce an incentive line on this graph:

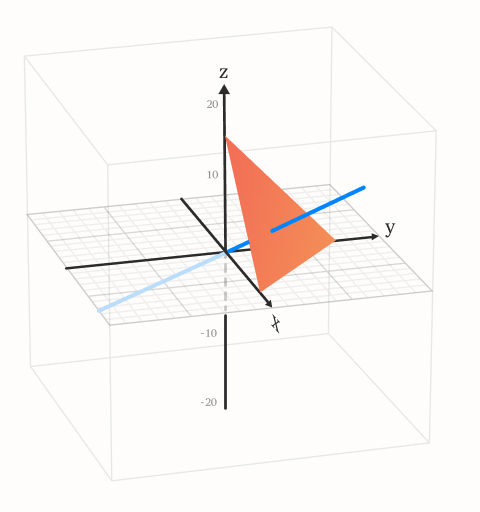
Figure 3: Iso-work domain (red) and the incentive line (blue)

The reputation function must reach a maximum on the presented domain exactly where the incentive line intersects it. A collection of points that have the same Reputation value are represented by the surface in this N-dimensional space. For the reputation to be maximal at the incentive line on a given domain the equi-Reputation surfaces must increase with value as one moves further from the origin which is guaranteed by the fact that Reputation should be monotonically increasing with the addition of more work.

Furthermore, equi-Reputation surfaces should be tangent to the domain W and touch it at only one point - the intersection point with the incentive line. This can only be possible if the reputation function is convex since if it was concave it would be also inside the pyramid the equi-work surface makes with the coordinate axis' and by definition would not have a unique incentive that does not belong to the coordinate planes. If it is convex one guarantees not only that reputation is maximal at the intersection point but it is maximal at that point for all possible amounts of imputed work that is lower than W.

To finalize the discussion let us list all properties the reputation function should have. It should be a continuous function that is monotonically increasing with the additional work imputed in any type of reputation. It should be convex and tangent to the equi-work line W and it should reach a maximum at the intersection point.

A method that we employ to prove that the conditions are met is Lagrange's multiplier. A function should reach a maximum given a constraint:

$g = x_{1} + x_{2} + ... + x_{N} - W$g=x1​+ x2​+...+ xN​−W

One function that is continuous, differentiable, and has modular behavior is the Balancer DEX invariant. It is of the form:

$R = x_{1}^{a_{1}} x_{2}^{a_{2}} ... x_{N}^{a_{N}}$R=x1a1​​ x2a2​​... xNaN​​

Let us prove that this function satisfies all necessary properties. The Lagrange multiplier method gives:

$gradR = \lambda * gradg$gradR=λ∗gradg

Which gives a set of N equations:

$\frac{∂}{∂x_{i}} x_{1}^{\alpha_{1}}x_{2}^{\alpha_{2}}...x_{N}^{\alpha_{N}}=\lambda*\frac{∂}{∂x_{i}}g = \lambda i \in [1, N]$∂xi​∂​x1α1​​x2α2​​... xNαN​​=λ∗∂xi​∂​g=λ i∈[1,N]

Which after solving for lambda gives a set of relations on variables and parameters:

$x_{i} / \alpha_{i} = x_{j} / \alpha_{j} \forall i,j \in [1, N]$xi​/αi​= xj​/αj​ ∀i,j ∈[1,N]

The incentive line condition can be found as:

$x_{1} / \alpha_{1} = x_{2} / \alpha_{2} = ... = x_{i} / \alpha_{i} = ... = x_{N} / \alpha_{N}$x1​/α1​= x2​/α2​=...= xi​/αi​=...=xN​/αN​

It is best to illustrate in 2D and 3D cases:

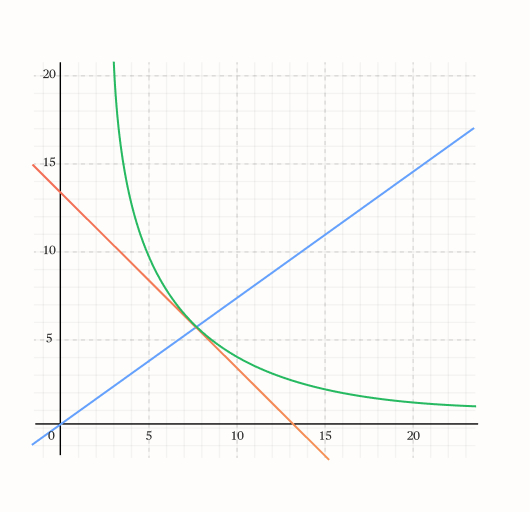
Figure 4: Maximization constraint with the iso-reputation curve (green) for N=2

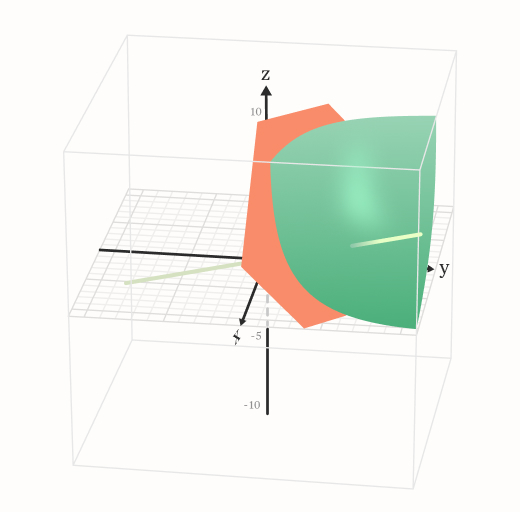
Figure 5: Maximization constraint with the iso-reputation curve (green) for N=3

The intersection between the domain W and some reputation function will always be a convex loop, for N=3 it can be visualized and it looks like this:

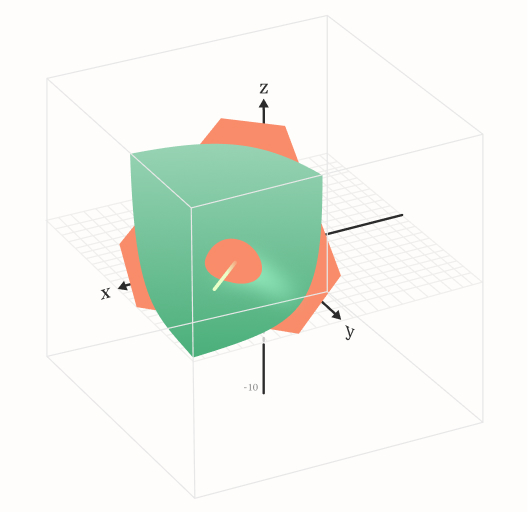
Figure 6: Convex loop at the intersection

The intersection of green and red surfaces, as displayed in Figure 6, determines all people that had imputed total work W and have the same reputation. As one increases the value of equi-Reputation, said loop will become smaller and smaller until eventually converging to the intersection point for the maximal Reputation users can have. It is now evident why the minimum of Reputation is set to 1. This is a mathematical practicality that implies that the specific reputations are independent and if a user has a minimal reputation of one type that does not impact his overall score negatively.

Addressing Temporal Dynamics

Let us now address the time dimension of a hypothetical reputation function. Should the reputation function have an upper bound? If it does not, after sufficient time some active users will accumulate so much reputation that new users will have little chance to catch up - think about it as a common condition of maximal attainable character level in MMORPGs. Had it not been bound, most of the games would have fallen out of favor after several years or would at a minimum, have resulted in severe inter-server fragmentation of active gamers.

This essentially is a problem of all merit-based systems, if qualitative work is additive then merit must be additive also. But if work is additive then early adopters benefit the most (which could be a desired property in some systems, but we shall concern ourselves with a more generalized case).

The only way to have a non-diverging meritocratic system is if we assume that the system has always been there - a condition that is impossible since we wish to create such a system. There is no general solution to this problem, but there may be a workaround. When designing the reputation function, we need to enable an option of diminishing returns, thus making reputation logarithmic in work input ensuring an easier entry to new users. Initially, a dynamical bound will exist and after sufficient time this constraint can be lifted by the community (e.g. using a 1P1V voting system).

Mathematics can get complex if one wishes to do this directly. A simpler approach can be to incorporate a decay directly in the reputation function. For example, consider how one reputation type $R$R depends functionally on the amount of points $X$X:

$R_{i} =x_{i}^{\alpha_{i}} for \alpha_{i} \in (0, 1)$Ri​=xiαi​​ for αi​∈(0,1)

Visualized:

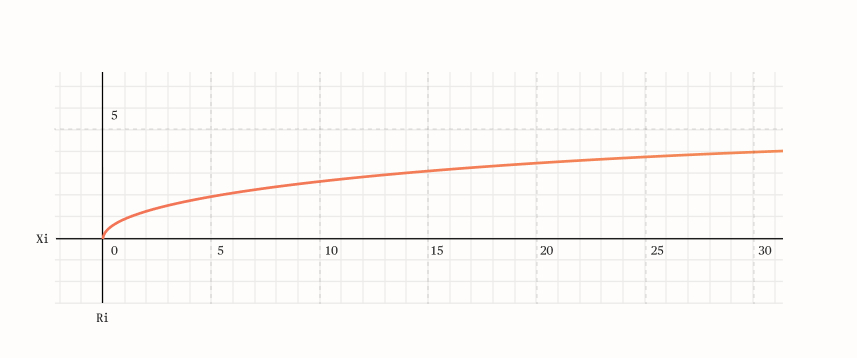
Figure 7: $\mathrm{<em>R</em>}\mathrm{<em>i</em>}$RiRi dependence on $\mathrm{<em>x</em>}\mathrm{<em>i</em>}$xiXi

The function does indeed possess diminishing returns, a fact one can see by taking a derivative of it:

$\frac{∂}{∂x_{i}} R_{i} = \alpha_{i} x_{i}^{\alpha_{i}-1} = \frac{ \alpha_{i} }{ x_{i}^{1 - \alpha_{i}} }$∂xi​∂​Ri​=αi​xiαi​−1​=xi1−αi​​αi​​

This shows that as $X_{i}$Xi​ increases the left-hand-side term continuously decreases thus for any (maximal work any given user can input in any given time frame, for example a month) $\delta>0$δ>0 $$there exists $x_{i}$xi​ such that:

$R_{i}(x_{i} + \Delta) - R_{i}(x_{i})<\delta$Ri​(xi​+Δ)−Ri​(xi​)<δ

This simple observation solves the problem of requiring an upper bound to reputation functions. If in a month a user loses more reputation to the decay than delta, the reputation will effectively have an upper bound. With this in mind let's define time decay.

Derivation via the Lagrange multiplier method must not be compromised when one incorporates time decay. Work variables need to be disconnected from time-dependent variables. When looking at the reputation function as a whole it is evident that the decay needs to act multiplicatively on all specific reputation functions respectfully. Mathematically, the specific reputation function with decay would look like this:

$R_{i}(x_{i},t)=x_{i}^{\alpha_{i}}*f_{i}(t)$Ri​(xi​,t)=xiαi​​∗fi​(t)

As decay acts on the function of work it is evident that the decay will have the same impact for all different $x_{i}$xi​ thus it will result in a % decrease in the specific reputation. Since:

$f(t) \in (f_{min}, 1]$f(t)∈(fmin​,1]

and$f(t)$ f(t) is monotonic and decreasing, inactive users lose reputation weight over time. As the decay is relative (i.e. percentage-based), the people with more reputation will lose more in absolute terms thus effectively decreasing the wedge between new and old users.

The simplest form would be a linear function:

$R_{i}(x_{i}, t) = MAX { 1, x_{i}^{\alpha_{i}} (1-k_{i}(t-t_{LatestAddition})) }$Ri​(xi​,t)=MAX { 1,xiαi​​(1−ki​(t−tLatestAddition​))}

The maximum function essentially does not impact the dynamics of the system but rather simply creates a lower bound that users can not cross, a box within the $XN$$$$X^N$XN space of specific reputations greater or equal to 1.

Let us now consider the problem that arises as a result of the functional form of decay. One must recognize that the total reputation of any type is essentially just a product of two functions, one that depends on qualitative work and the other that is only time-dependent. As arguably they are independent, the time component will always tend to reduce the amount of reputation linearly.

As discussed earlier, people will deploy their productive time into work but their returns will diminish with every incremental unit of work done. This implies that at some point people will move so far along the curve that no matter what they do they will not be able to increase their reputation further or even keep it from declining. After sufficient time all people would find themselves with their reputation equal to 1. This corollary creates evident challenges when considered from the vantage point of system incentives.

This problem can not be solved directly but rather with an algorithm:

1. Let us say that a user holds $X$X amount of total work and that as of this moment, their reputation of type $i$i is:

$R_{i}(x_{i},t)=X^{a_{i}}$Ri​(xi​,t)=Xai​

2. As time progresses a user loses reputation linearly:

$R_{i}(x_{i}, t) = x_{i}^{\alpha_{i}} (1-k_{i}(t-t_{LatestAddition}))$Ri​(xi​,t)=xiαi​​(1−ki​(t−tLatestAddition​))

3. On the next increment of work, a user has:

$R_{i}(x_{i}, t) = X^{\alpha_{i}} (1-k_{i}(t_{CurrentAddition}-t_{LatestAddition}))$Ri​(xi​,t)=Xαi​(1−ki​(tCurrentAddition​−tLatestAddition​))

4. Effective work would then equal to:

$X_{eff.} = \lbrace R_{i}(x_{i},t) \rbrace^{\frac{1}{\alpha_{i}}} = \lbrace X^{\alpha_{i}} (1-k_{i}(t_{CurrentAddition}-t_{LatestAddition})) \rbrace^{\frac{1}{\alpha_{i}}}$Xeff.​={Ri​(xi​,t)}αi​1​={Xαi​(1−ki​(tCurrentAddition​−tLatestAddition​))}αi​1​

5. The reputation of type i would then be equal to:

$R_{i}(x_{i},t) = \lbrace X_{eff.} + \Delta \rbrace^{\alpha_{i}}$Ri​(xi​,t)={Xeff.​+Δ}αi​

6. Total work would then be equal to:

$X_total = X + Delta$$Xtot. = X + Delta$$X_{tot.} = X + \Delta$Xtot.​=X+Δ

7. As time progresses it evolves as:

$R_{i}(x_{i},t) = \rbrace X_{eff.} + \Delta \rbrace^{\alpha_{i}} (1-k_{i}(t_{CurrentAddition}-t_{LatestAddition})$Ri​(xi​,t)={Xeff.​+Δ}αi​(1−ki​(tCurrentAddition​−tLatestAddition​))

This algorithm is not particularly complex; it simply ensures that due to the time decay, effectively, people move along the reputation curve. It is best to illustrate in a scheme in which a user can always increase the input work without any change to the 'difficulty' (which arises from the fact that the first derivative of any reputation type is monotonically decreasing). This is illustrated by the example that the user will always need the same amount of work to position oneself at the position one once was if one does this periodically:

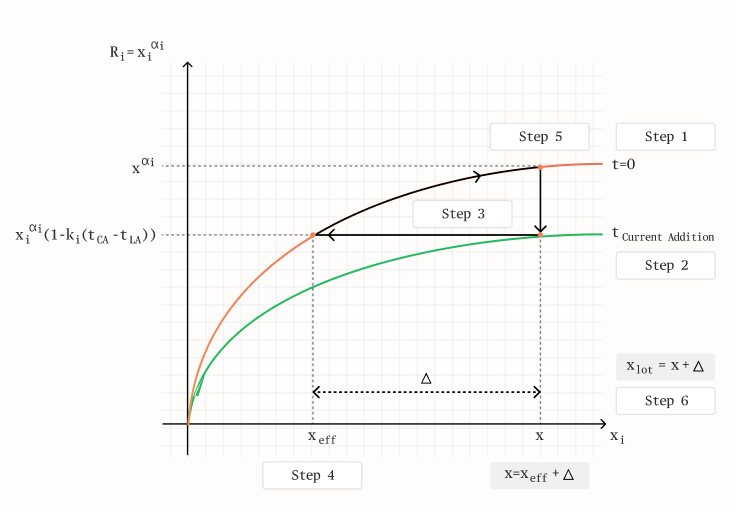
Figure 8: Time decay algorithm

Addressing Dynamic Incentives

The model that has been derived so far possesses a unique incentive line that is fixed throughout time, see Figure 5. This is great, but cannot accommodate a simple and ubiquitously desired property of dynamic weights with smooth transitions. That is to say that if we want to create reputation functions that can dynamically adjust in the face of changing circumstances while ensuring smooth interstate transition, our math has to allow for that.

As a protocol progresses the desired incentives may change which shall result in a redistribution of weights resulting in a change in the slope of the incentive line to any of the axes. If one defines the reputation in absolute terms, the consequence of a dynamic incentive line would be an abrupt change in realized user reputation - all of a sudden some will have more, and others will have less. Aside from an evident user experience problem, there is a more subtle one. Assuming agents strive to maximize their reputation, it becomes a game of prediction of future weights rather than a game of maximizing reputation under current conditions, thus incentives become distorted.

There is also an ideological problem: the system is not meritocratic if all reputation that someone has accumulated becomes negligible at some point in time. The way to mitigate this problem, and ensure that the people that were following the incentives all of the time are the ones that are rewarded the most, even in cases of dynamic weights, is to make reputation continuously accrue - i.e. dynamic.

The way to achieve this is to define reputation in dynamic terms - the rate of reputation accrual per block:

$\Delta R_{i}(x_{i}, t) = x_{i}^{\alpha_{i}}(1-k_{i}(t-t_{LatestAddition}))$ΔRi​(xi​,t)=xiαi​​(1−ki​(t−tLatestAddition​))

$\Delta R_{i} = R_{1} R_{2}...R_{N}$ΔRi​=R1​R2​...RN​

$\Delta R(x_{1},x_{2}, ..., x_{N}) = \displaystyle\prod_{I=1}^n x_{i}^{\alpha_{i}}(1-k_{i}(t-t_{LatestAddition}))$ΔR(x1​,x2​,...,xN​)=I=1∏n​xiαi​​(1−ki​(t−tLatestAddition​))

The decay mechanism is kept in this transition. If at a given point in time, users behave optimally (they behave like the function incentivizes them to) they will be rewarded the most then. Ones that are at an optimal position (in the sense of the distribution of work) all of the time will certainly have the most.

A careful reader would note a small detail. Since everything is defined up to an increment that can be non-zero at all times the global reputation function now is not bounded. But yet again it has diminishing returns for larger values of work. This area is that of ongoing research at the time of publishing of this paper.

There are some candidate solutions: one can incorporate a global time decay or non-additive components into the reputation function. One of those can be a simple parameter solution:

Let us denote increments of reputation (the continuously accruing component) at time $ti$ti​ as $Ri=R(ti)$ ΔRi​= ΔR(ti​) . The protocol accrues information about these increments and denotes their sum: ∑i​​ΔRi​

$i delta Ri$$$$$$$$$$$$$$$$$$$$$
i​$\sum_{\substack{i}} \Delta R_{i}$

The total reputation score is a function of this sum: $R = R ($R=R(∑i​​ΔRi​$)$)
$\Delta$$R_{i}$

This ensures that users, effectively, move along the reputation curve while accruing reputation increments. As this restriction is global it should not impact the optimal behavior of users within the system since their optimality condition stays intact.

While addressing the issues of inter-temporal congruence of incentives, this way of calculating reputation is completely exogenous to the dynamics of the system.

A Note on Negative Reputation

An important note to add here is that although the reputation function is defined in positive-only terms, it does not imply that this functional form cannot be used for enabling some sort of negative reputation scores. In our view, from a game theoretical viewpoint, there must be disincentives to malicious actions, although there must also be a right to be forgotten that can be enacted under certain circumstances.

A wider discussion on the philosophical aspects of negative reputation and the entire problem space of privacy matters evolving around it is far beyond the scope of this article, yet we still would like to address this issue from a vantage point of the mathematical model presented above.

In general, there are two ways to incorporate negative reputation into the model - either by reducing the total work that has been performed by the user (which will reduce his/her reputation as a consequence) or by exogenously decreasing the user's reputation score directly. The first solution reduces the user's work but does not impact his/her 'difficulty' in obtaining more reputation points. The second does not impact the amount of work a user has done but increases the 'difficulty' of accruing more reputation since the model gives the reputation as an output and is not impacted by its end values. It is a hard choice between these two options since the solution needs to be implementable in code but also fair. Further research is being performed in this area.

A Note on One-off and Continuous Reputation

Work performed is transcribed via the table to the number of points. From the protocol's perspective only points matter thus we are treating these points as work in the sense that they are additive. Tables are composed of tasks (actions) and their point rewards.

There are 2 kinds of tasks: One-off tasks and Continuous tasks.

One-off tasks can be done only once thus they must not be submitted to the decay function. If they were then after sufficient time they would have no impact on users' reputation and the final result would not be meritocratic. On the other hand, if they are not subject to time decay they would farm reputation indefinitely and create progressively bigger differences between the users.

The way to solve this problem is to split reputation into two parts: a one-off part and a continuous part. The one-off part has no time decay but it does not farm reputation - it is a scalar that effectively translates the reputation function in the $R+$$\Re^+$ℜ+ space.

The continuous part has time decay and it has all the properties that had been derived until now. Thus, the functional form of the one-off reputation part is the same as R just without the decay. Table 1 as seen below, illustrates the differences between these two types of reputations:

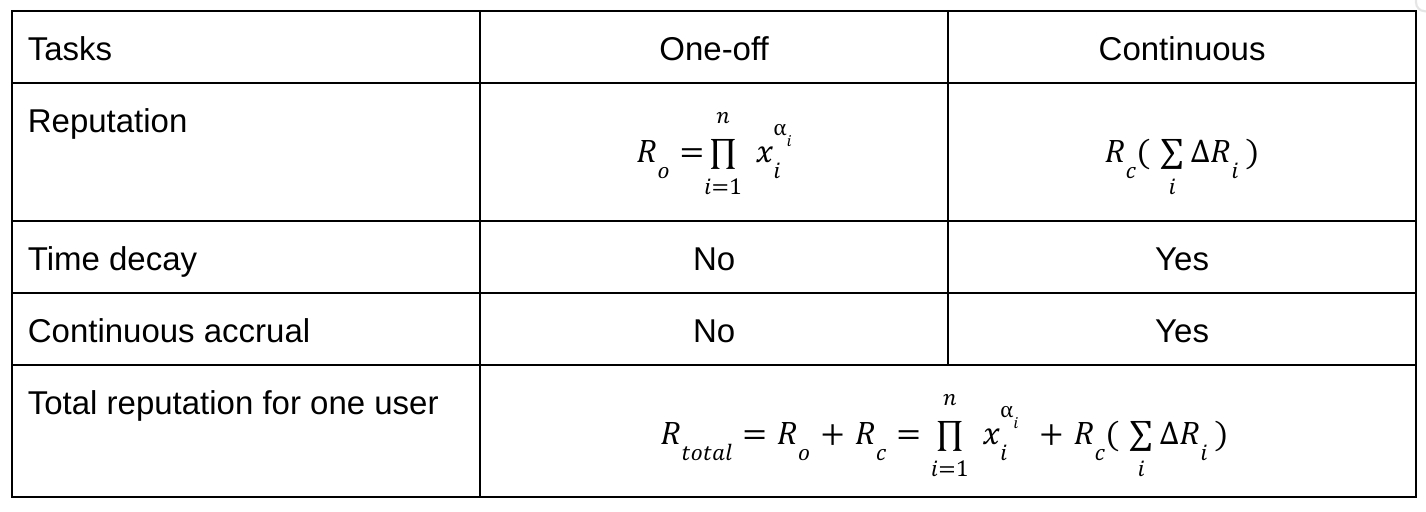
Table 1: Difference between one-off and continuous tasks